Home > Topdrawer > Fractions > Misunderstandings > Fractions as a double count > Fraction fiddle
Fraction fiddle
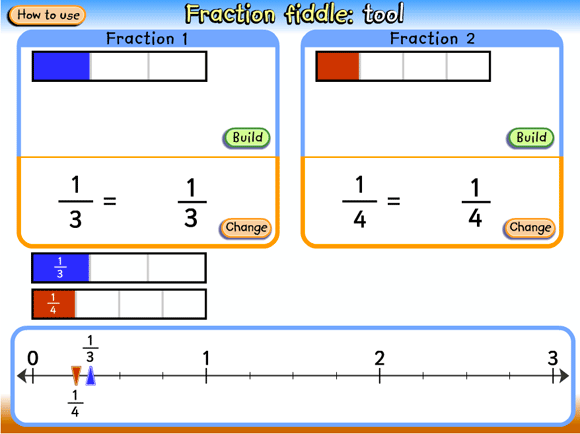
Display the learning object L2800 Fraction fiddle: tool to the class on an interactive whiteboard (or projector and screen).
Screen grab from L2800 Fraction fiddle: tool.
Source: © Education Services Australia Ltd, 2011
- Enter a fraction (e.g. \(\frac{1}{3}\)) and discuss how a bar can be constructed to represent that fraction.
- Point out that the length of the bar is the same as the distance between 0 and 1 on the number line, and so helps to locate the fraction on the number line. The fraction bar acts as a bridge from the typical area model for representing fractions to a linear model.
- Select another fraction (e.g. \(\frac{1}{4}\)) and ask students to predict what the bar diagram will look like, and where the fraction will be located on the number line. Ask questions such as:
- Will \(\frac{1}{4}\)be smaller or larger than \(\frac{1}{3}\)?
- Will \(\frac{1}{4}\) be closer to 1 than \(\frac{1}{3}\)?
- Emphasise the fact that, together, the numerator and denominator form a number that has a value, and therefore a place on the number line.
