Home > Topdrawer > Geometric reasoning > Good teaching > Exploring congruence
Exploring congruence
Shapes which can be superimposed on each other are said to be congruent. They are the result of a rotation, translation or reflection or a combination of these transformations. Congruent shapes are used extensively in design.
- Explore real life patterns such as those in tiling and patchwork.
Patterned floor tiles.
Source: Getty/Pete Ryan.
- Cut out shapes from within a design and place them on top of each other.
- Discuss the sequence of transformations required to map one shape onto another: translation, rotation and reflection.
- Use pattern blocks to construct designs based on congruence.
- Provide students with a cut-out of a specific shape which they can use to re-draw the shape in a new orientation.
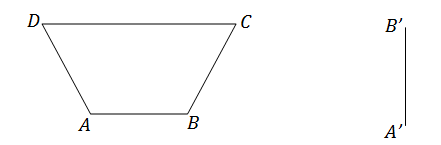
For example, draw ABCD in the new orientation indicated by A’B’.
Subsequently, provide students with activities which require them to draw transformations of shapes without the aid of a real object.
Students find challenge in constructing designs which involve rotations.
- Provide objects which can be manipulated physically to assist.
- Use polar grid paper to complete the rotation and then trace the resulting shape onto square grid paper.
- Highlight the matching sides and angles in different colours to ensure that they are equal.
Developing the congruence tests
In order to establish the minimal conditions under which triangles are congruent, explore all triangles which satisfy three given conditions.
